Did you know Joey Votto in 2012 had the highest ratio of doubles as a percentage of balls in play in the history of baseball? 400 or more plate appearances; Votto had 475, but only 374 at bats, and in those 374 he had 14 homers and 85 strikeouts, so now we’re down to 275 balls in play. In those 275 he hit 44 doubles. That’s 160 doubles per 1000 balls in play, which is the highest ratio in the history of baseball.
Perhaps of more interest. …the 2013 Red Sox had two of the highest ratios of all time. Until 2013, Jarrod Saltalamacchia had never hit doubles; it was one of the notable things about him, that he hit no doubles. In 2012, playing two-thirds of the games, he hit only one double in July and none at all in August. In 2013, for unknown reasons, he became a doubles machine, bashing 40 doubles on 272 balls in play—the second-highest ratio ever, behind only Votto. Mike Napoli, with 39 doubles on 288 balls in play in 2013, was 10th on the list.
Of course Fenway is a great place to hit doubles, but on the other hand, people have been playing in Fenway for a hundred years. The record-holder for doubles, Earl Webb with 67 in 1930,
a) Played in Fenway, and
b) Hit 128 doubles per 1000 balls in play, which used to be a really impressive number.
Webb was third on the list through 1993, behind Ned Williamson (1883) and Hank Greenberg (1934); now he is 13th.
* * * * *
Did you ever notice that the words "spatter" and "splatter" appear to be used interchangeably and with almost equal frequency? As I was finishing up Popular Crime I noticed that I had used "splatter" when all the cool people seemed to be using "spatter", so I changed them all to spatter. But since then I notice that many people actually use "splatter"; it seems as common as the other. Seems odd; in essence the two words are rhyming synonyms.
In the era of book I’m working on now (a little more than a hundred years ago) the word "clue" is spelled "clew" about 90% of the time.
* * * * *
I have written several times about "families" of pitchers, which is kind of a frustrating concept because I can’t quite get it right, so I keep going back to it. I have finally realized that one of the reasons I can’t get it right is that I keep trying to define families as discrete cells, non-overlapping, when in reality families have very imprecise boundaries. If A and B are part of the same family and B and C are part of the same family, this does not mean that A and C are part of the same family; B could be a nephew of A and a cousin of C although A and C have no connection, have never met and never heard of one another; that’s actually common. The same problem with pitchers; Doyle Alexander can be represented as a part of the same family of pitchers as Joe Niekro, and Niekro as a part of the same family of pitchers as Jim Lonborg, and this does not necessarily imply that Doyle Alexander is a part of the same family of pitchers as Jim Lonborg.
Related to the first problem, I have been representing all familial relationships among pitchers as being the same, as perhaps they were all brothers. I realize now that actually the concept of "families" of pitchers is actually more workable if we remember that families have all different kinds of relationships—father to son, brother to brother, brother to sister, first cousins, second cousins, grandfathers, nieces and nephews, etc.
It would be convenient if we could (but of course we can’t). . ..if we could represent starting pitchers as male and relievers as female. Claude Osteen and Tom Burgmeier, for example, are in many respects profoundly similar, but we don’t tend to think of them as members of the same pitching family because Osteen was a starter and Burgmeier a reliever. We should think of them as siblings but not brothers.
Except, of course, that there is too much baggage involved with describing a male athlete in female terms. Just wrestling with the concept. . .I don’t have anywhere to go with it right now. Carl Hubbell is Fernando Valenzuela’s grandfather. I used to work with a guy who was Carl Hubbell’s actual grandson, but you get my point.
* * * * *
OK, my main purpose today is to re-visit the concept of "Player Skills Age". I know I have written about this before, and I never know how much tolerance my audience has for my habit of going back to the same areas of research again and again. I do it, though, because I’ve made some progress, or think that I have. It’s a normal research pattern; you work on something, make a little progress, put it aside, go back to it when you have another insight. It’s normal, but the fact that it is normal doesn’t make it interesting. My job description requires that I be interesting; otherwise people stop reading.
Anyway, Player Skills Age. Suppose that we could place a number on the age of a player’s skills. In other words, Michael Bourn to Run and Albert Callaspo in 2013 were both 30 years old, and were similar in terms of overall effectiveness, Bourn hitting .263 with 6 homers, 50 RBI, and Callaspo hitting .258 with 10 homers, 58 RBI. Baseball Reference credits Callaspo with 0.5 WAR and Bourn with 1.9, but that difference is mostly defense.
Callaspo and Bourn are the same age and at similar levels as hitters, but Callaspo’s skills are obviously much "older" than Bourn’s. Bourn hit six triples and stole 23 bases; Callaspo had no triples and no stolen bases. Bourn had 40 walks and 132 strikeouts; Callaspo had exceptional control of the strike zone for a modern player, with 53 walks and only 47 strikeouts. Bourn grounded into 2 double plays; Callaspo, 12.
Bourn has "younger skills" than Callaspo, but what is the difference? How "old" are Bourn’s skills? How "old" are Callaspo’s skills?
Bourn’s "skill age" is 21.9; Callaspo’s is 33.9. Bourn’s skills, in effect, are 12 years younger than Callaspo’s.
How did we arrive at that conclusion? It was a long loop and I wasted a lot of time. I don’t want to waste your time, so in short: I began by identifying to what extent each area of production is associated with aging, identified eight "skill indicators", and cooked up a way to tag each one to a specific age.
None of that is exactly true; it’s short hand. I actually didn’t begin by identifying to what extent each area of production is associated with aging; I began by assuming that I already knew that, and then later, in the middle of the study, realized that I should study the issue, which turned out to be very useful. Also, I didn’t really identify eight different skill indicators; I created eight indicators, but they overlap to a large extent and really just come down to speed and control of the strike zone.
A few things I learned from the internal studies. First, I was using power as an age indicator. While power does increase somewhat as players age, power cannot effectively be used as an age indicator because the individual (player to player) differences in power are so much larger than the chronological (age to age) differences that the predictable chronological changes in power are of very little use in assessing a player’s age. In other words, if you compare let’s say Dave Kingman and Jerry Remy. . .Dave Kingman at some age is faster than Jerry Remy at some age. Jerry Remy throughout his career was much faster than Dave Kingman, but Dave Kingman at the age of 20 was faster than Jerry Remy at the age of 35. This is generally but not quite universally true. Harmon Killebrew at the age of 18 was faster than Luis Aparicio at the age of 40, although Aparicio was tremendously fast and Killebrew was tremendously not fast.
But the same is not true of power, not at all. There is no age comparison at which Jerry Remy has more power than Dave Kingman, no age at which Luis Aparicio has more power than Harmon Killebrew. So power is not useful in scaling age in the same way that speed is; this is one of the things I realized from doing this particular study, although I did keep power in the process at a very confined level.
Another thing I realized like that is that I was going the wrong way with strikeouts. I was assuming that strikeouts increase as a player ages. I was assuming that because it is true at a certain point in a player’s exit path. A 35-year-old player will strike out more than a 32-year-old player.
But it is more untrue than it is true; strikeouts decrease with experience somewhat longer than they increase, so that to the extent you can use strikeouts as an indicator of age, strikeouts indicate youth, rather than age. If you divide a player’s career in the middle—or anyplace close to the middle—in more cases than not you will find that the player has a higher strikeout rate BEFORE the divide than after. It’s not lopsided; some player’s strikeout rate increases and some decrease, but it decreases more often than it increases.
So my first "age indicator system" didn’t work worth a crap, because I was treating power as an indicator of age, which is so unreliable that it merely churns the data, and also I was going the wrong way with strikeouts. At some point it occurred to me that I should actually stop and study the extent to which various performances indicated age, and then I made some progress. Another thing I found was that doubles are of no use as an indicator of age; I had assumed that to be true, and then I studied it and found that it was true. Also, stolen base percentage, it turns out, is (apparently) useless as an indicator of age. In my earlier systems I was using all speed indicators as age indicators, but while the other speed indicators are extremely useful age indicators, stolen base percentage doesn’t change with age enough to make it useful (although there could be something there I am missing if stolen base percentage was combined with the number of attempts.)
Anyway, I wound up with eight indicators of a player’s "skills age". I’ll describe them first, give you the formulas second, and the weights assigned to each indicator third. The eight indicators are:
1) Triples as a percentage of balls in play,
2) Strikeout to Walk ratio,
3) Stolen Base Attempt Frequency,
4) Strikeouts Relative to Home Runs,
5) Walk Rate (unrelated to strikeouts),
6) Runs Scored as a Percentage of Times on Base/Not Home Run,
7) Grounded into Double Play Rate, and
8) Strikeout Rate (unrelated to walks or home runs).
The "skill age" assigned to each of these eight indicators cannot be less than 18 or more than 42, so if you use one of the formulas below and get an out-of-range result, just move it back to the boundary. This next section of this article is complicated and boring, so feel free to skip it; I’ll put in a picture of Juan Samuel as a marker, and you can just jump ahead now to Juan Samuel if you want to; you won’t miss anything vital.
1. Triples as a Percentage of Balls in Play
Multiply Triples as a Percentage of Balls in Play by 1000, and subtract from 42, so that the more triples a player hits, the younger the "skills age" we assign to him. Andy Van Slyke in 1994 hit 12 triples in 614 at bats. Van Slyke had 14 homers and 99 strikeouts, so that’s 12 triples with 501 balls in play, or .023981, or 23.981 triples per 1000 balls in play. Subtract that from 42; that 18.019, so Van Slyke’s "Skill Age Score 1" (SKA1) is 18.019. If he had hit another triple, we’d have to flatten him out at 18.
2. Strikeout to Walk Ratio
Divide the player’s walks, plus five, by his strikeouts, walks and ten (BB + 5) / (SO + BB + 10). Multiply that by 32, and add 14. Miguel Olivo in 2007 had 14 walks and 123 strikeouts; that makes 19/147, or .129252. Multiply by 32, you’ve got 4.136054; add 14 and you’re at 18.13604, so Olivo’s "Skill Age Score 2" (SKA2) in 2007 is 18.13604. Only two players in history (400 or more plate appearances) would score at less than 18 without the mandated move back to 18—Miguel Oliva in 2006, and Ivan Rodriguez in 2007.
We add the 5 and 10 into the formula so that 10 strikeouts and 1 walk doesn’t score the same as 100 strikeouts and 10 walks. When you have more data, you have more confidence in the data. We have more confidence that a strikeout/walk ratio of 100-10 is a "real" skill measurement than we do in 10-1.
3. Stolen Base Attempt Frequency
Figure the player’s stolen base attempts as a percentage of his times on base not including home runs (SB + CS) / (H + W + HBP – 2B – 3B – HR). Multiply this number by 100, and subtract from 42. Alexei Ramirez in 2013 had 39 stolen base attempts. He had 181 hits, 26 walks and was hit by pitches 3 times, so he was on base 210 times. Of those 210, however, 47 were extra base hits (39-2-6), so he had 39 stolen base attempts with 163 times on first base, or .239264. Multiply that by 100 (23.9264) and subtract from 42, you get 18.0736, so Ramirez’ "Skill Age Score 3" (SKA3) is 18.0736. If he had attempted one more stolen base, we’d have to flatten him out at 18.
4. Strikeouts relative to Home Runs
Divide Strikeouts by the total of Home Runs, Strikeouts and 25. Multiply that number by 30, and subtract from 45. The more a player strikes out (relative to his homers) the "younger" we will score his skills; the more homers he hits (relative to his strikeouts) the "older" we will score his skills. Austin Jackson, International Man of Mystery, struck out 170 times in 2010 and hit 4 home runs, which makes 170 over 199, or .854271. Multiply by 30 and subtract from 45; that makes 19.37, so his "Skill Age Score 4" (SKA4) is 19.37. That makes him the "youngest" player in baseball history on this scale. Johnny Mize in 1947 had 51 homers and 42 strikeouts. That makes 42 / (42 + 51 + 25), or .355932. Multiply that by 30 and subtract from 45, you get 34.32, so Mize’s Skill Age Score 4 is 34.32.
5. Walk Rate (Unrelated to Strikeouts)
Figure the player’s Walks per plate appearances. Multiply that by 100, and add to 18. Mark McGwire in 1998 walked 162 times in 681 plate appearances. That’s .237885, or 23.7885 walks per 100 plate appearances. Add that to 18; that’s 41.7885, so McGwire has a "Skill Age Score 5" (SKA5) of 41.7885. One or two more walks, we’d have had to flatten him out at 42.
6. Runs Scored as a Percentage of Times on Base
Figure the player’s Runs Scored, not including Home Runs, as a percentage of times on base, not including Home Runs. Multiply that by 100, and subtract that from 53. Kevin Seitzer in 1988 had 170 hits, 72 walks and was hit by pitches 6 times, so he was on base 248 times. He scored 90 runs, but 5 of the 90 were home runs, so he scored 85 runs in 243 times out base. That’s a very high rate of runs scored/times on base. That’s .349794, or 34.9794 runs scored per 100 times on base. Subtract that from 53; it’s 18.0206, so Seitzer’s "Skill Age Score 6" (SKA6) is 18.0206. If he had scored one more run, we’d have to flatten him out at 18.
You may be suspicious of the notion of scaling age by Runs Scored, but my research shows that younger players do in fact score more runs as a percentage of times on base than older players. Much of that is probably derivative of other effects; younger players hit more triples, are used as pinch runners rather than being pinch run for, and are more often used in the top-of-the-order batting positions that have an advantage in run scoring. Whatever the cause, I don’t care; I’m just exploiting the information to the best of my ability.
7. Grounded Into Double Play Rate
Figure how many double plays the player has grounded into, per 500 balls in play. Add that number to 16, so that the more double plays a player grounds into, the older the "skill age" we assign to him. Rico Carty in 1979 (The Beeg Boy) grounded into 21 double plays in 461 at bats. He had 12 homers and 45 strikeouts, so that’s 21 double plays in 404 balls in play, which is 25.9901 double plays per 500 balls in play. Add 16, that’s 41.9901, so Carty’s "Skill Age Score 7" (SKA7) is 41.9901. If he had grounded into one more double play, we’d have to flatten him out at 42. (As someone who actually remembers seeing Rico Carty play in 1979, I must say that he looked much older than 41.9901.)
8. Strikeout Rate (Unrelated to Walks)
Divide Strikeouts by Plate Appearances. Multiply that by 100, and subtract from 45. Cory Snyder in 1987 struck out 166 times in 615 plate appearances, which is a) too many strikeouts, and b) .269919, or c) 26.9919 strikeouts per 100 at bats. Subtract that from 42; that’s 18.0081, so Snyder’s "Skill Age Score 2" (SKA2) is 18.0081. If he’d struck out one more time, we’d have to list him as an 18-year-old.
OK, having figured the 8 "Skill Age Scores", we combine them, giving the most weight to those which are most strongly correlated with actual age.
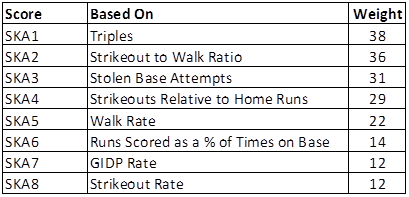
Don’t ask me to explain how I derived those weights; I’m not that good a mathematician. The total weight is 194 points for players for whom we have Grounded Into Double Play data, 182 for the older players for whom GIDP data is not available. Triples account for about 20% of the overall score; strikeout rate accounts for 6%.

By this process, the "youngest" skill set in my data (since 1920) was by Juan Samuel in 1984. Samuel—actually 23 years old in 1984—had a "skill set age" of 19.55. He hit 19 triples, stole 72 bases in 87 attempts, and had a strikeout/walk ratio of 168 to 28. His eight "Skill Age Components" are 18.0, 19.1, 18.0, 20.8, 21.8, 18, 21.8, and 22.2. The ten "youngest" players in the data are Juan Samuel, 1984; Starling Marte, 2013; Juan Samuel, 1986; Lou Brock, 1963; Willie Wilson, 1988; Lou Brock, 1966; Sammy Sosa, 1990; Juan Samuel, 1985; Peter Bourjous, 2011, and Omar Moreno, 1983. Maybe I should have given you some of their stats:
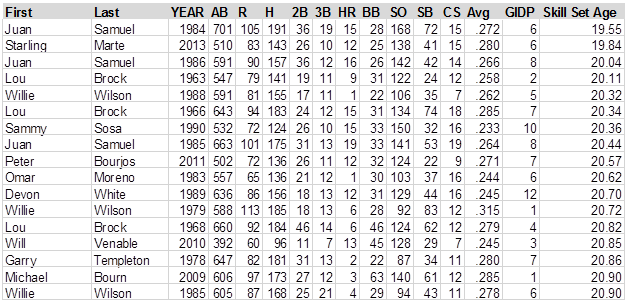
I extended the chart a little bit to make the point that Willie Wilson scores as a very young player in 1979 (skill set age of 20.72), but scores as even younger nine years later (20.32). This brings up a question: is this even related to actual age? I’ll deal with those kind of questions in a moment.
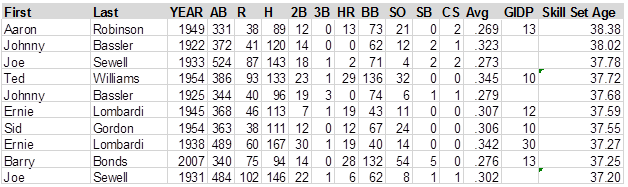
Aaron Robinson in 1949 hit no triples and stole no bases in 2 attempts. He completely commanded the strike zone, getting 73 walks with only 21 strikeouts (13 homers), grounded into 13 double plays (a very high rate), and scored only 38 runs in 110 games, an absurdly low rate for a player with a .402 on base percentage. He thus scores as the "oldest" player—the oldest skill set—in my data, with a "Skill Set Age" of 38.4. The ten "oldest" players in my data are as follows:
Actually, just because I like doing this stuff, I’m going to print lists of the "youngest" and "oldest" players at each age. . . .in other words, the youngest and oldest 25-year-olds, etc. Some of the "zero" GIDP in these charts should show as blanks:
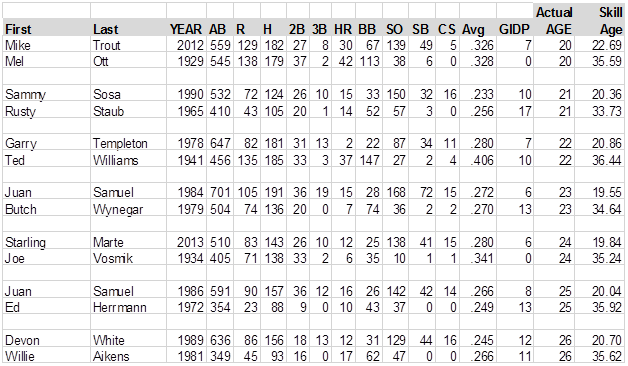
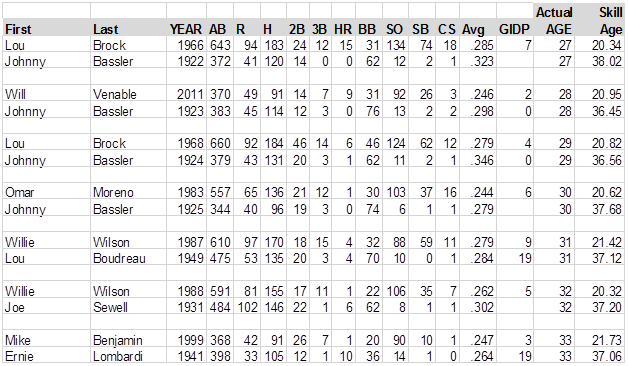
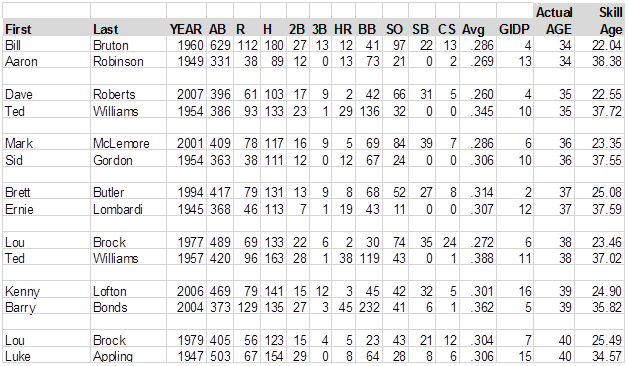
Mark McLemore in 2001 was the youngest 36-year-old in the history of baseball, while Sid Gordon in 1954 was the oldest 36-year-old in the history of baseball; stuff you would never know if you didn’t read BJOL. But the chart raises a question, as well. The "oldest" 21-year-old ever was Rusty Staub in 1965, but then Staub played for 20 years after that. The "oldest" 22-year-old was Ted Williams in 1941, but Williams played another 19 years. Maybe, if you want players who will stay around a long time, you shouldn’t look for young player’s skills, but old player’s skills?
I’ll deal with those kind of questions in a minute. Also, not that many of you would know this or would care, but Johnny Bassler, who shows as the oldest 27-year-old, the oldest 28-year-old, the oldest 29-year-old and the oldest 30-year-old in the data, actually played very good baseball in the Pacific Coast League until he was in his mid-forties, I think. I should observe at some point that of course we should round off Skill Ages to the nearest integer, since it is a very imprecise process, and a two-decimal estimate of a Wild Ass Guess is borderline pretentious, but if we rounded them off, we’d lose the chart above; you’d have a bunch of 32-year-old players whose skills were 37 years old, and no way to choose one of them as "the oldest" 32-year-old. Are we done here? OK. . . .let me get to the questions I have been dodging.
First, do these scores actually increase as the players age? Yes, they do. This chart shows the average "skill age" at each calendar age from 20 to 39:
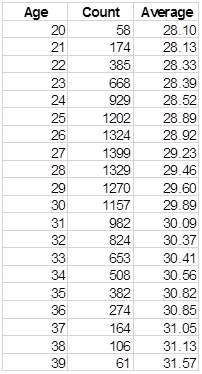
In all of the area where we have 50 or more players, the average "skill set age" is higher for each calendar age than for the one before.
Of course, it doesn’t go up at a 1-to-1 level. It can’t, because the difference between the skill packages of different players is far more substantial than the differences between skills at different ages. But it does go up.
If you focus on an individual player, you do find in a general way that his skill set age increases as his calendar age increases. Let’s look at, for example, at Andruw Jones:
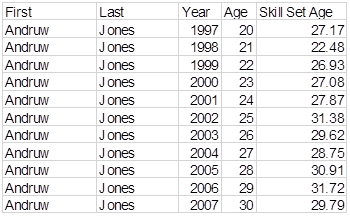
His "Skill Set Age" doesn’t always go up, but it generally goes up. The first five years average 27.15; the last five years average 29.98. Let’s do Chipper:
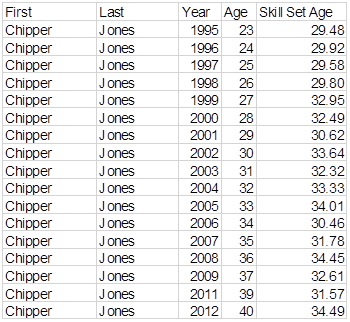
If you compare a random player in Year 1 to the same player in Year 2, the player will have an older skill set in Year Two 57% of the time. If you compare the same player two years apart, Year 1 and Year 3, he will have an older skill set in Year three 63% of the time. If you compare Year 1 and Year 4, the player in Year 4 will have an older skill set 67% of the time.
If you compare a random player in Year 1 to the same player in Year 2, the player will have an older skill set in Year Two 57% of the time. If you compare the same player two years apart, Year 1 and Year 3, he will have an older skill set in Year three 63% of the time. If you compare Year 1 and Year 4, the player in Year 4 will have an older skill set 67% of the time.
I repeated that paragraph because I thought it was important.
OK, finally, the biggest question: If you compare a player with "young player’s skills" to a player with "old player’s skills", does the player with young player’s skills have a "future" advantage?
Yes, he does. The advantage is not large; it’s not the first "sorting variable" you would look at in choosing players. But there is a meaningful advantage to the player who has young player’s skills.
I am sure I have studied this issue before, but I’m also sure that I have never studied it this well before. Until now I have never had a tool to say how "mature" a player’s skills were. Armed with this tool, I did a matched-set study. I identified 206 sets of players, based on similarity of age, runs created and outs made, but dissimilarity in Skill Set Age. For example, Garry Templeton in 1977 and Greg Gross in 1974:

Garry Templeton and Greg Gross in 1974 were both 21 years old, and each player created 85 runs. They made about the same number of outs.
Gross, however, had much more mature skills than did Templeton. Templeton hit 18 triples and stole 28 bases; Gross hit 8 triples and stole only 12 bases, although it was not for want of trying. Templeton’s strikeout/walk ratio was 70-15; Gross’s was 39-76. The players were the same age and equal as hitters, but Greg Gross was a much older 21.
Gene Richards in 1978 and Mark McGwire in 1988; Richards’ skill set was much younger than McGwire’s:

Dave Parker in 1976 and Richie Hebner in 1973; Parker’s skill set was much younger than Hebner’s:

Andre Dawson in 1982 and Roger Maris in 1962:

Andy Van Slyke in 1987 and Matt Lawton in 1998:

Kirk Gibson in 1984 and Fred McGriff in 1991:

In all 206 cases, we paired players who were the same age and who created exactly the same number of runs, in all cases with minor differences or no differences in the number of outs made. But in every case we have contrasted a player with young player’s skills with a player whose skills were at a more mature level. No players were included in the study from 2004 or later, so that we could "look ahead" at what the player did in the rest of their careers.
The theory is that there might be individual differences in each of the 206 cases; one player might be injured the next season, or one player might be having a fluke season not representative of his ability, or the run context might be very different so that the player’s run contribution is not as well matched as it appears. There might be any number of such differences in individual cases, but when you study 206 of them, those things should begin to relatively even out, leaving the groups separated only by the inherent advantage (or disadvantage) of having young skills as opposed to mature skills. It’s also a lot of fun. . . .Pokey Reese winds up matched with Earl Battey, Devon White with Paul Konerko, Vince Coleman with Don Wert; just crazy stuff that you would never come up with on your own.
When we aggregate the past and future performance of the "Type 1" and "Type 2" players in this study, it is apparent that the "Mature Skills" players have been better, in the previous seasons, than the "Young Skills" players, but that the Young Skills players have somewhat brighter futures. The "Mature Skills" players, through the base year of the study, had played an average of 750 career games, had hit 62 home runs, averaged .278, and had a .757 OPS. The "Young Skills" players, through the base year of the study, had played an average of almost 100 fewer games (651) with a lower batting average (.271), fewer home runs (44), and a substantially lower OPS (.731). The "mature skills" players, because their skills were more mature, reached the majors at a younger age than did the "young skills" players.
But when we look to the rest of their careers, after the base year of the study, the players with Young Player’s Skills played more games (798 to 717) with a higher batting average (.262 to .255) and a higher OPS (.713 to .705). They even hit more home runs, in the rest of their careers, 64 to 62, although this is only because they hung around longer.
The Young Skills Players had more stolen bases both through the base year and after the base year. Through the base year the advantage was 134 to 27; after the base year it was 114 to 10.
With regard to the Rusty Staub/Ted Williams issue that I mentioned earlier and promised to discuss, the central fact of "aging" in baseball is that quality equals survival. Those players who are able to play until they are 40 years old, 90% of the time, are simply the best players. The players who can survive until they are 40 are the players who are so good that even when they lose 10, 15 points off their batting average, as everybody does, even when they lose their speed, even when they become more prone to injuries and thus more inconsistent, they can still play because they’re still above the line. Most players, when they lose a little bit, they’re gone. Willie Mays loses a step, you live with it. That truth does more to explain aging in baseball than everything else you can know about the subject.
Those players who are most exceptional are also, of course, those players whose skills mature at an early age. The rules which govern exceptional players are not the same as those which govern ordinary players.
This is a secondary effect that we’re dealing with here, an "ordinary players" effect—but it is not a small effect, either. Given a certain and known level of ability—superstar compared to superstar, or bench guy compared to bench guy--you’re better off with a player with young player’s skills than a player with old player’s skills. The "Young Skills" group, in this study, played 11% more games in the remainder of their careers, a difference (in this study) of 17,000 career games. What it comes down to, really, is defense. The fast player who loses a step is still fast enough to play the outfield. The slow player who loses a step steps over a line; now he is just too slow. That’s really the main advantage of young player’s skills.